ランダムな数の発生方法-04-2

誤差関数を使って表してみる

\(\Large Rand_{0-1} = \frac{1}{ \sqrt{ \mathstrut 2 \ \pi \ \sigma^2}} \int_{-\infty}^x e^{- \frac{t^2}{2 \sigma^2}}　dt \)　

誤差関数は，

\(\Large erf (x) = \frac{1}{ \sqrt{ \pi }} \int_{0}^x e^{- t^2}　dt \)　

ですので，変数変換して，

\(\Large \frac{t^2}{2 \sigma^2} \equiv w^2 \ \rightarrow \frac{t}{\sqrt{2} \sigma} = w \ \rightarrow \ \frac{dt}{\sqrt{2} \sigma} = dw\)　

\(\Large 0 \sim t \sim x\)　

\(\Large 0 \sim \ w \sim \ \frac{x}{\sqrt{2} \sigma} \)　

となるので，

\(\Large Rand_{0-1} = \frac{1}{ \sqrt{ \mathstrut 2 \ \pi \ \sigma^2}} \displaystyle \int_{-\infty}^{x / \sqrt{2} \sigma} e^{- w^2}　dw \cdot \sqrt{2} \sigma \)　

\(\Large = \frac{1}{ \sqrt{ \pi }} \displaystyle \int_{-\infty}^{x / \sqrt{2} \sigma} e^{- w^2}　dw \)　

\(\Large = \frac{1}{ \sqrt{ \pi }} \left[ \displaystyle \int_{-\infty}^{0} e^{- w^2}　dw + \int_{0}^{x / \sqrt{2} \sigma} e^{- w^2}　dw\right] \)　

誤差関数から，

\(\Large erf (- \infty) = \frac{1}{ \sqrt{ \pi }} \displaystyle \int_{0}^{- \infty} e^{- t^2}　dt = -1\)　

\(\Large \displaystyle \int_{0}^{- \infty} e^{- t^2}　dt = - \frac{ \sqrt{ \pi}}{2} \rightarrow \displaystyle \int_{- \infty}^0 e^{- t^2}　dt = \frac{ \sqrt{ \pi}}{2} \)　

となるので，

\(\Large Rand_{0-1} = \frac{1}{ \sqrt{ \pi }} \left[ \displaystyle \int_{-\infty}^{0} e^{- w^2}　dw + \int_{0}^{x / \sqrt{2} \sigma} e^{- w^2}　dw\right] \)　

\(\Large = \frac{1}{ \sqrt{ \pi }} \left[ \frac{ \sqrt{2}}{2} + \frac{ \sqrt{2}}{2} \cdot erf \left(\frac{x}{ \sqrt{2} \sigma} \right) \right] \)　

\(\Large = \frac{1}{ 2} \left[ 1 + erf \left(\frac{x}{ \sqrt{2} \sigma} \right) \right] \)　

となります．誤差関数の逆関数を，erf^-1，とすると

\(\Large erf \left(\frac{x}{ \sqrt{2} \sigma} \right) = 2 Rand_{0-1}-1 \)　

\(\Large \frac{x}{ \sqrt{2} \sigma} = erf^{-1} (2 \ Rand_{0-1}-1) \)　

\(\Large x = \sqrt{2} \sigma \cdot erf^{-1} (2 \ Rand_{0-1}-1) \)　

となり，０から１のランダム関数と誤差の逆関数を用いれば，正規分布の各点を求めることができます．

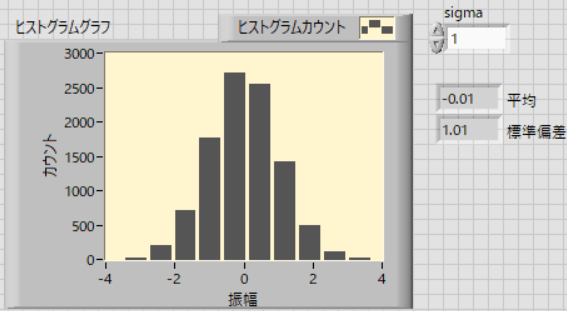
実際に，σ=1，で１万回，試行したところ，

のように，標準偏差が１，の正規分布となりました．

実際のプログラムでどう扱うかを次ページに示していきます．